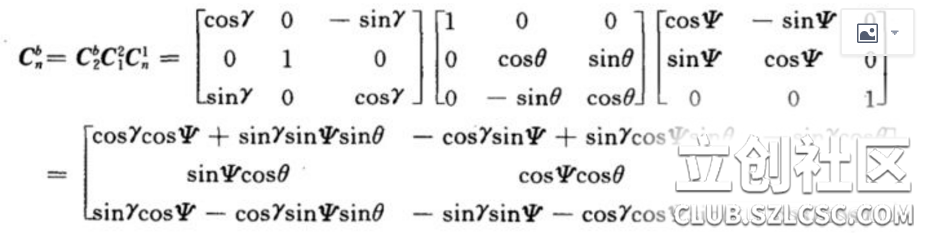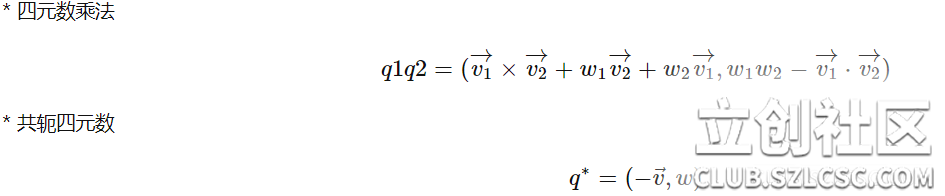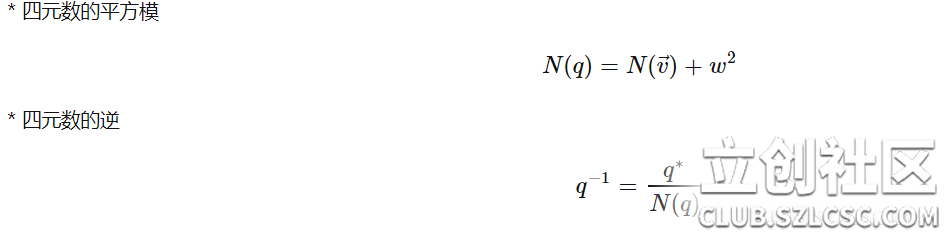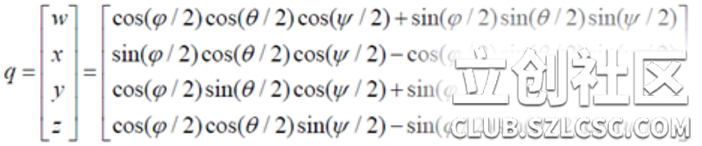|
查看:
8895
|
回复:
4
|
基于MPU6050的姿态解算算法入门
|
||||||


晏几台char
13
主题
6
回复 |
1#
电梯直达

众所周知,我们可以通过MPU6050可以获得姿态角,即偏航角、横滚角和俯仰角。但要注意的是,所谓的欧拉角只是姿态角的一个子集,飞机姿态角是由机体坐标系与地理坐标系之间的关系确定的,姿态,即一个坐标系到另一个坐标系的转换关系。有这样的概念,对于我们理解姿态解算是有好处的,建立起立体几何的概念模型。 我们所谓的姿态解算,也就是获取姿态角和采用某种数学模型表示出来,更通俗点说,MPU6050相当于一个输入端,为了处理数据,在MCU中,作为输出端必须对这些数据进行表示。 姿态角归根到底,是一个角,单位是°,而我们所用的这个MPU6050是基于三种角速度传感器+三轴加速度传感器,它所测量的值是角速度和加速度,并未角度,如对于速度的积分是路程一样,角速度的积分就是角度;这里的加速度也是指重力加速度,并非运动加速度。 由于MPU6050不具备三轴地磁场传感器,所以这里只作简单介绍。地磁场传感器,又称磁力计,它提供了正北方向的参考。 角速度,重力加速度和地磁场这三个传感器结合到一起,可以各自弥补本身的不足。 角速度传感器所求出来的角度是由积分算出来的,那么,静止的时候必然出现稳定的累计误差,我们也称静差,恰好,重力加速度传感器在静止的时候,算出的重力加速度没有运动加速度的影响,所以,重力加速度的值很准确,但我们也发现,飞行器在水平方向静止的不动的时候,重力加速度传感器是测不到水平上的加速度的,也就是偏航角的值无法保证,此时我们可以用地磁场传感器来测出偏航角的变化值。 这三个传感器互相取长补短,我们便可以获得比较准确的姿态角了。 获得到姿态角后,我们如何将姿态角表示出来,方便我们处理呢。 1、欧拉角 2、余弦矩阵 3、四元数 1、 欧拉角 欧拉角是最直观的,即俯仰角(Pitch)、横滚角(Roll)和偏航角(Yaw)。 一般旋转顺序是先yaw后pitch,再roll反应到坐标轴上就是先绕Z轴旋转,再绕X轴旋转,最后绕Y轴旋转。 需要注意的是 yaw pitch roll 都是对应的固定的参考系 也就是上面说的地理坐标系而言,每次新的姿态坐标系都是由地理坐标系通过欧拉角旋转得到的。 什么是万向节死锁? 如下图一,把灰色箭头想象成是一架飞机,红,绿蓝三个圈看作是三个外围控制器,外圈带动所有里圈运动,里圈的运动不影响外圈。 1,首先,绕Y轴旋转(旋转绿圈),来确定前进的方向。这时红圈与蓝圈都跟着旋转。 2,然后,绕x轴旋转(旋转红圈),让飞机仰视或俯视。这时蓝圈跟着一起旋转,绿圈不动。 3,最后,绕z轴旋转(旋转蓝圈),让飞机左右倾斜。这时只有蓝圈在转,红绿圈不动。 经过这三个步骤,我们可以把飞机调整到任意想要的角度。这也是FPS相机中常用的 yaw, pitch, row三个操作。 在步骤2中,若旋转红圈过程中,恰巧旋转到了图二所示状态,然后进行步骤3时会发现,旋转蓝圈与绿圈效果一样。 也就是这种状态下,旋转Y或Z轴效果一样了,都只能使飞机左右倾斜,而不能再俯视或仰视(它只能头朝天),这下坏了,飞机操作失灵了,只能向上直冲。这就所谓的万向节死锁,gimbal lock. 可见,欧拉角旋转使用的是物体的局部坐标系,旋转过程是对局部坐标的三个轴X,Y,Z分别进行的旋转。 【所谓的死锁,仅是在一个操作单元,即XYZ组成的任意一个次序中出现了无法控制的现象,如上面飞机失灵的情况,我们可以继续操作X轴(红圈)来调整飞机的仰视和俯视,这时飞机又可以回到水平飞行的正常轨道上来了】 【但是,对于使用欧拉角旋转的程序,没有人会去专门写逻辑来判断是否发生了万向节死锁,D3D底层API更不会去管,因此我们的程序就会出BUG] yaw 是左右看,pitch是俯视或仰视,roll就是左右倾斜。 如果我们写了一个FPS的飞机控制程序,当发生上面的死锁时,调用pitch就与调用roll一样了,当发现飞机朝上飞时,于是调用pitch想调整机头朝下,结果却发现飞机只是左右倾斜而机头仍然朝上直飞!出BUG了。 2、 方向余弦矩阵 我们先将飞机坐标系中的x轴拿出来,来分析它位于地理坐标系的位置,记为X’,由于之前我们通过对于角速度的积分求得了旋转的角度α,那么,在地理坐标系XYZ中,例如单位向量X’在地理坐标系XYZ上都存在一个投影。 我们先只研究飞机坐标系的X轴,假设,先绕Z轴旋转,旋转的角度α就是X和X’的夹角,如图。
由于X’是单位向量,简单地,我们可以得到关于X’的三阶矩阵。
这里要说一下矩阵的含义,C2 1表示坐标系 1 到坐标系 2 的变换矩阵,那么有
这样我们可以得到3个变换矩阵
分别为单独绕Z轴旋转,绕X轴旋转,绕Y轴旋转。 实际上,两坐标系任何复杂的角位置关系都可以看做有限次基本旋转的组合,变换矩阵 等于基本旋转确定的变换矩阵的连乘(线性代数), 连 乘的基本顺序依据基本旋转的顺序向右排列。
不会矩阵乘法的,请看定义。
最后的矩阵就是完整的余弦矩阵。γ、θ、ψ就是欧拉角啦。 至此我们解释了为什么欧拉角会有旋转的顺序之分。从以上数学计算可以看出不同的旋转次序会带来不同的结果。
每一行所代表的是
3、 四元数 一个四元数可以表示为q = w + xi + yj + zk,其中w为实部,i,j,k为虚部,x,y,z为系数,其中四元数乘法满足: i*i=j*j=k*k=i*j*k=-1 i*j=k j*i=-k j*k=i k*j=-i k*i=j i*k=-j 四元数是一个四维空间上的量,为方便表示,我们使用q = ((x, y, z),w) = (v, w),其中v是向量,w是实数,这样的式子来表示一个四元数。 四元数可以看做是向量和实数的一种更加一般的形式,向量可以视作为实部为0的四元数,而实数可以是作为虚部为0的四元数。上述四元数的运算性质也是实数或向量的运算性质的更一般的形式。
可以推导出四元数的一些运算性质,包括:
附上三维向量的叉乘和点乘公式:
它的证明这里不再赘述,有兴趣的可以参见这篇文章。主要思想是构建了一个辅助向量k,它是将p绕旋转轴旋转θ/2得到的。证明过程尝试证明wk?=kv?,以此证明w与v、k在同一平面内,且与v夹角为θ。
我们举个最简单的例子:把点P(1, 0, 1)绕旋转轴u = (0, 1, 0)旋转90°,求旋转后的顶点坐标。 1、 首先将P扩充到四元数,即p = (P, 0)。 2、 q = (u*sin45°, cos45°)。求 建议大家一定要在纸上计算一边,这样才能加深印象,连笔都懒得动的人还是不要往下看了。 3、最后的结果p` = ((1, 0, -1), 0),即旋转后的顶点位置是(1, 0, -1)。 如果想要得到复合旋转,只需类似复合矩阵那样左乘新的四元数,再进行运算即可。 我们来总结下四元数旋转的几个需要注意的地方: 1、用于旋转的四元数,每个分量的范围都在(-1,1)。 2、每一次旋转实际上需要两个四元数的参与,即q和q*; 3、所有用于旋转的四元数都是单位四元数,即它们的模是1; 欧拉角到四元数的转换
四元数到欧拉角的转换
arctan和arcsin的结果是
那么,在实践中是怎样的呢?我们接下来先了解一些名词。 AHRS是自动航向基准系统(Automatic Heading Reference System)的简称。目前,使用四元数来进行AHRS姿态解算的算法被广泛采用于四轴飞行器上。该算法源自英国Bristol大学的Ph.D Sebastian Madgwick,他在2009年开发并发布了该算法。下面我们来对该算法的代码进行详细分析。
IMU是惯性测量装置(Inertial Measurement Unit)的简称,通常包含陀螺仪和加速度计。(MPU9150还包括磁力计) 现在,让我们回到姿态解算代码的分析。下述代码的核心思想是:通过陀螺仪的积分来获得四轴的旋转角度,然后通过加速度计的比例和积分运算来修正陀螺仪的积分结果。 重力加速度归一化(规范化)(normalization),就是转化为标量,即只有数值大小,没有方向,在IMU中是将三维向量转化成单位向量,因为单位矢量到参考坐标系的投影,所以要把加速度计数据单位化, 四元数表示转动,首先其模应该为1,
下面代码中的gx,gy,gz分别代表陀螺仪在X轴,Y轴和Z轴三个轴上的分量,ax,ay,az分别代表加速度计在在X轴,Y轴和Z轴三个轴上的分量。 void MahonyAHRSupdateIMU(float gx, float gy, float gz, float ax, float ay, float az) { float recipNorm; //归一化、规范化的中间变量 float halfvx, halfvy, halfvz; //重力的值 float halfex, halfey, halfez; //偏差程度 float qa, qb, qc; 只有当加速度计测量有效时才计算反馈(避免在加速度计正常化时使用NaN) // Compute feedback only if accelerometer measurement valid (avoids NaN in accelerometer normalisation) if(!((ax == 0.0f) && (ay == 0.0f) && (az == 0.0f))) { invSqrt为平方根的倒数,原因是使得下面的ax,ay,az的运算速度更快。通过归一化处理后,ax,ay,az的数值范围变成-1到+1之间。 归一化化加速度计测量 // Normalise accelerometer measurement recipNorm = invSqrt(ax * ax + ay * ay + az * az); ax *= recipNorm; ay *= recipNorm; az *= recipNorm; 根据当前四元数的姿态值来估算出各重力分量。用于和加速计实际测量出来的各重力分量进行对比,从而实现对四轴姿态的修正。 // Estimated direction of gravity and vector perpendicular to magnetic flux halfvx = q1 * q3 – q0 * q2; halfvy = q0 * q1 + q2 * q3; halfvz = q0 * q0 – 0.5f + q3 * q3; 使用叉积来计算估算的重力和实际测量的重力这两个重力向量之间的误差。 // Error is sum of cross product between estimated and measured direction of gravity halfex = (ay * halfvz – az * halfvy); halfey = (az * halfvx – ax * halfvz); halfez = (ax * halfvy – ay * halfvx); 把上述的累计误差进行积分运算,就可以消除累积误差。 // Compute and apply integral feedback if enabled if(twoKi > 0.0f) { integralFBx += twoKi * halfex * (1.0f / sampleFreq); // integral error scaled by Ki integralFBy += twoKi * halfey * (1.0f / sampleFreq); integralFBz += twoKi * halfez * (1.0f / sampleFreq); gx += integralFBx; // apply integral feedback gy += integralFBy; gz += integralFBz; } else { integralFBx = 0.0f; // prevent integral windup integralFBy = 0.0f; integralFBz = 0.0f; } 把上述计算得到的重力差进行比例运算。比例的结果累加到陀螺仪的数据中,用于修正陀螺仪数据。比例系数为Kp。 // Apply proportional feedback gx += twoKp * halfex; gy += twoKp * halfey; gz += twoKp * halfez; } 至此,我们得到了修正后的数据,然后我们需要将这些数据,表示到四元数中。 // Integrate rate of change of quaternion gx *= (0.5f * (1.0f / sampleFreq)); // pre-multiply common factors gy *= (0.5f * (1.0f / sampleFreq)); gz *= (0.5f * (1.0f / sampleFreq)); qa = q0; qb = q1; qc = q2; //一阶近似算法 q0 += (-qb * gx – qc * gy – q3 * gz); q1 += (qa * gx + qc * gz – q3 * gy); q2 += (qa * gy – qb * gz + q3 * gx); q3 += (qa * gz + qb * gy – qc * gx); 把上述运算后的四元数进行归一化处理。得到了物体经过旋转后的新的四元数。 // Normalise quaternion recipNorm = invSqrt(q0 * q0 + q1 * q1 + q2 * q2 + q3 * q3); q0 *= recipNorm; q1 *= recipNorm; q2 *= recipNorm; q3 *= recipNorm; } 
我是一个粉刷匠,粉刷本领强。
|
||||||

微风吹过山野
1
主题
22
回复 |
2#
看不到插图。。。

|
||||||


晏几台char
13
主题
6
回复 |
3#
等我修改一下。

我是一个粉刷匠,粉刷本领强。
|
||||||


晏几台char
13
主题
6
回复 |
4#
众所周知,我们可以通过MPU6050可以获得姿态角,即偏航角、横滚角和俯仰角。但要注意的是,所谓的欧拉角只是姿态角的一个子集,飞机姿态角是由机体坐标系与地理坐标系之间的关系确定的,姿态,即一个坐标系到另一个坐标系的转换关系。有这样的概念,对于我们理解姿态解算是有好处的,建立起立体几何的概念模型。 我们所谓的姿态解算,也就是获取姿态角和采用某种数学模型表示出来,更通俗点说,MPU6050相当于一个输入端,为了处理数据,在MCU中,作为输出端必须对这些数据进行表示。 姿态角归根到底,是一个角,单位是°,而我们所用的这个MPU6050是基于三种角速度传感器+三轴加速度传感器,它所测量的值是角速度和加速度,并未角度,如对于速度的积分是路程一样,角速度的积分就是角度;这里的加速度也是指重力加速度,并非运动加速度。 由于MPU6050不具备三轴地磁场传感器,所以这里只作简单介绍。地磁场传感器,又称磁力计,它提供了正北方向的参考。 角速度,重力加速度和地磁场这三个传感器结合到一起,可以各自弥补本身的不足。 角速度传感器所求出来的角度是由积分算出来的,那么,静止的时候必然出现稳定的累计误差,我们也称静差,恰好,重力加速度传感器在静止的时候,算出的重力加速度没有运动加速度的影响,所以,重力加速度的值很准确,但我们也发现,飞行器在水平方向静止的不动的时候,重力加速度传感器是测不到水平上的加速度的,也就是偏航角的值无法保证,此时我们可以用地磁场传感器来测出偏航角的变化值。 这三个传感器互相取长补短,我们便可以获得比较准确的姿态角了。 获得到姿态角后,我们如何将姿态角表示出来,方便我们处理呢。 1、欧拉角 2、余弦矩阵 3、四元数
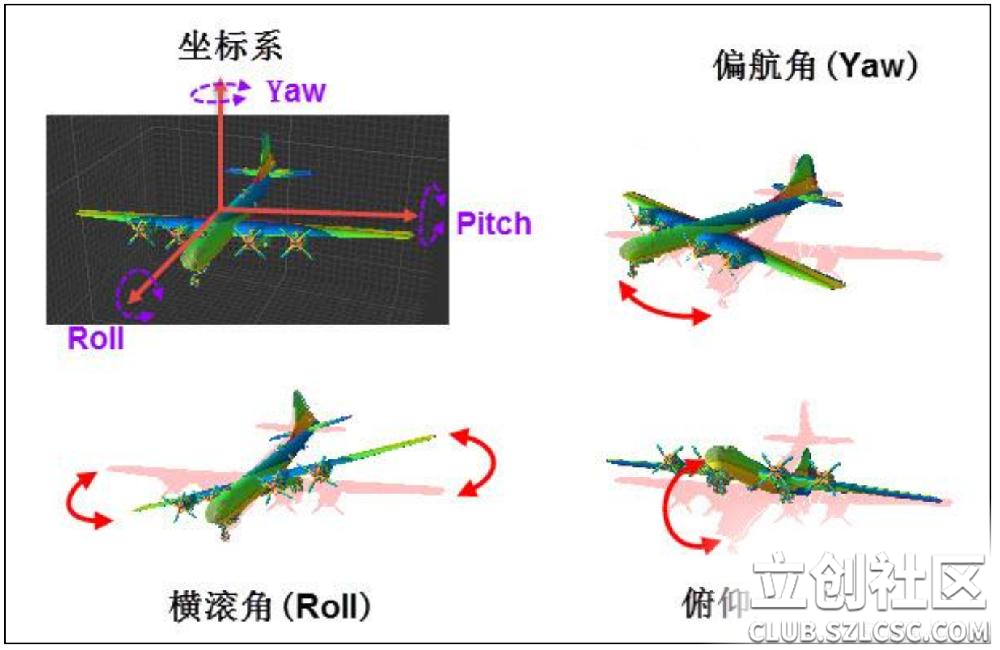
1、 欧拉角 欧拉角是最直观的,即俯仰角(Pitch)、横滚角(Roll)和偏航角(Yaw)。 一般旋转顺序是先yaw后pitch,再roll反应到坐标轴上就是先绕Z轴旋转,再绕X轴旋转,最后绕Y轴旋转。 需要注意的是 yaw pitch roll 都是对应的固定的参考系 也就是上面说的地理坐标系而言,每次新的姿态坐标系都是由地理坐标系通过欧拉角旋转得到的。
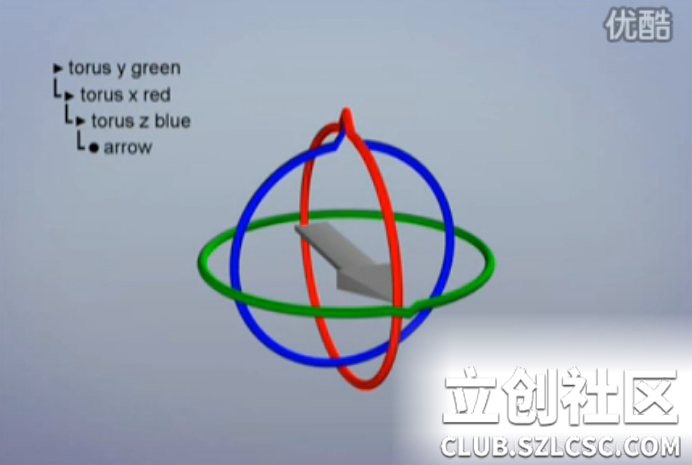
什么是万向节死锁? 如下图一,把灰色箭头想象成是一架飞机,红,绿蓝三个圈看作是三个外围控制器,外圈带动所有里圈运动,里圈的运动不影响外圈。
1,首先,绕Y轴旋转(旋转绿圈),来确定前进的方向。这时红圈与蓝圈都跟着旋转。
2,然后,绕x轴旋转(旋转红圈),让飞机仰视或俯视。这时蓝圈跟着一起旋转,绿圈不动。
3,最后,绕z轴旋转(旋转蓝圈),让飞机左右倾斜。这时只有蓝圈在转,红绿圈不动。 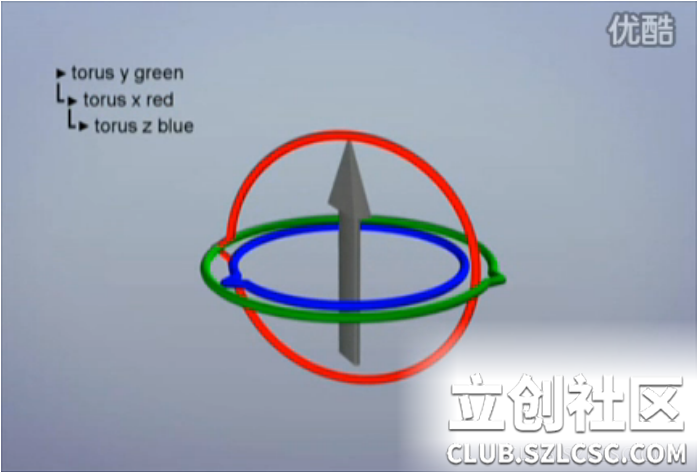
经过这三个步骤,我们可以把飞机调整到任意想要的角度。这也是FPS相机中常用的 yaw, pitch, row三个操作。
在步骤2中,若旋转红圈过程中,恰巧旋转到了图二所示状态,然后进行步骤3时会发现,旋转蓝圈与绿圈效果一样。
也就是这种状态下,旋转Y或Z轴效果一样了,都只能使飞机左右倾斜,而不能再俯视或仰视(它只能头朝天),这下坏了,飞机操作失灵了,只能向上直冲。这就所谓的万向节死锁,gimbal lock.
可见,欧拉角旋转使用的是物体的局部坐标系,旋转过程是对局部坐标的三个轴X,Y,Z分别进行的旋转。
【所谓的死锁,仅是在一个操作单元,即XYZ组成的任意一个次序中出现了无法控制的现象,如上面飞机失灵的情况,我们可以继续操作X轴(红圈)来调整飞机的仰视和俯视,这时飞机又可以回到水平飞行的正常轨道上来了】
【但是,对于使用欧拉角旋转的程序,没有人会去专门写逻辑来判断是否发生了万向节死锁,D3D底层API更不会去管,因此我们的程序就会出BUG]
yaw 是左右看,pitch是俯视或仰视,roll就是左右倾斜。
如果我们写了一个FPS的飞机控制程序,当发生上面的死锁时,调用pitch就与调用roll一样了,当发现飞机朝上飞时,于是调用pitch想调整机头朝下,结果却发现飞机只是左右倾斜而机头仍然朝上直飞!出BUG了。
1、 方向余弦矩阵 我们先将飞机坐标系中的x轴拿出来,来分析它位于地理坐标系的位置,记为X’,由于之前我们通过对于角速度的积分求得了旋转的角度α,那么,在地理坐标系XYZ中,例如单位向量X’在地理坐标系XYZ上都存在一个投影。 我们先只研究飞机坐标系的X轴,假设,先绕Z轴旋转,旋转的角度α就是X和X’的夹角,如图。 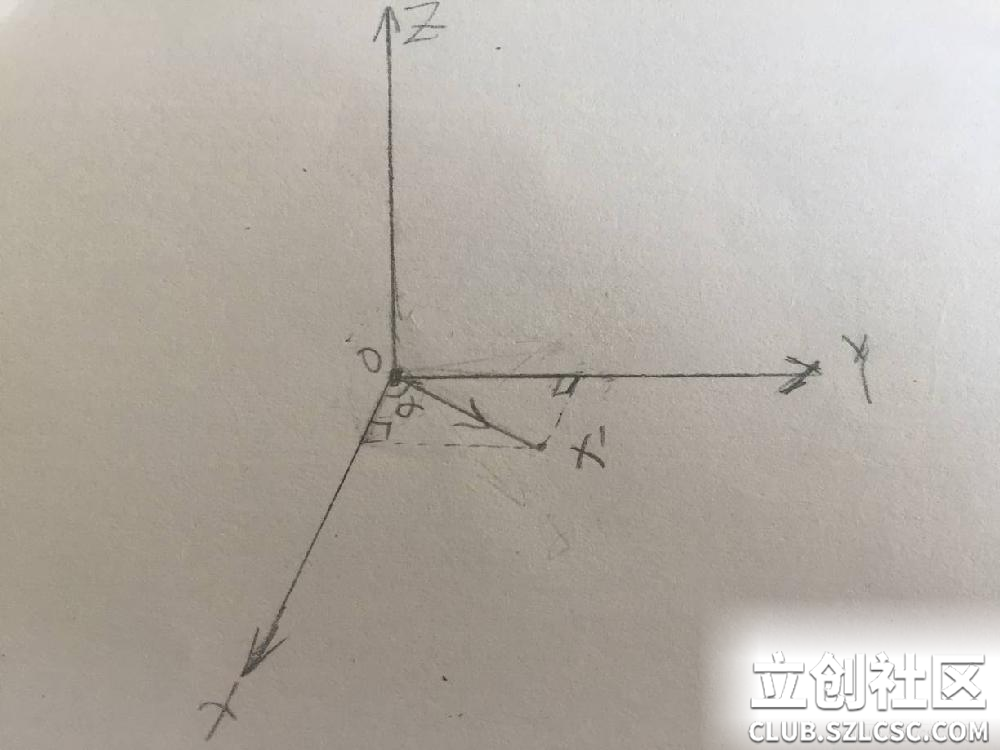
由于X’是单位向量,简单地,我们可以得到关于X’的三阶矩阵。 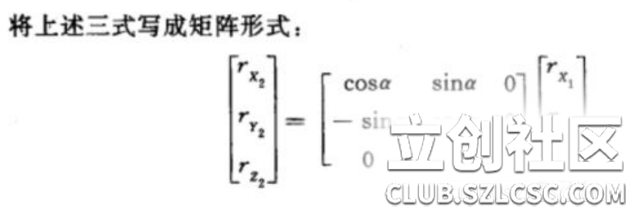
这里要说一下矩阵的含义,C2 1表示坐标系 1 到坐标系 2 的变换矩阵,那么有 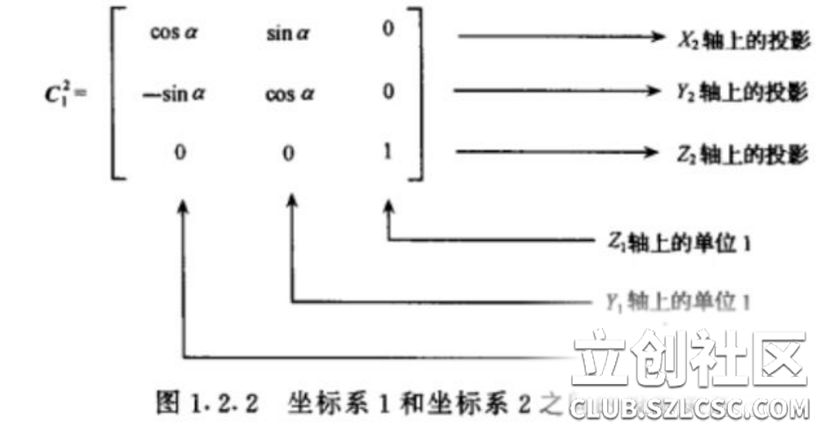
这样我们可以得到3个变换矩阵 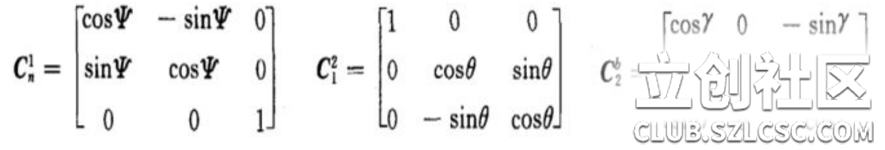
分别为单独绕Z轴旋转,绕X轴旋转,绕Y轴旋转。 实际上,两坐标系任何复杂的角位置关系都可以看做有限次基本旋转的组合,变换矩阵 等于基本旋转确定的变换矩阵的连乘(线性代数), 连 乘的基本顺序依据基本旋转的顺序向右排列。

最后的矩阵就是完整的余弦矩阵。γ、θ、ψ就是欧拉角啦。 至此我们解释了为什么欧拉角会有旋转的顺序之分。从以上数学计算可以看出不同的旋转次序会带来不同的结果。
每一行所代表的是

我是一个粉刷匠,粉刷本领强。
|
||||||


晏几台char
13
主题
6
回复 |
5#
3、 四元数 一个四元数可以表示为q = w + xi + yj + zk,其中w为实部,i,j,k为虚部,x,y,z为系数,其中四元数乘法满足: i*i=j*j=k*k=i*j*k=-1 i*j=k j*i=-k j*k=i k*j=-i k*i=j i*k=-j 四元数是一个四维空间上的量,为方便表示,我们使用q = ((x, y, z),w) = (v, w),其中v是向量,w是实数,这样的式子来表示一个四元数。 四元数可以看做是向量和实数的一种更加一般的形式,向量可以视作为实部为0的四元数,而实数可以是作为虚部为0的四元数。上述四元数的运算性质也是实数或向量的运算性质的更一般的形式。 附上三维向量的叉乘和点乘公式:
它的证明这里不再赘述,有兴趣的可以参见这篇文章。主要思想是构建了一个辅助向量k,它是将p绕旋转轴旋转θ/2得到的。证明过程尝试证明wk?=kv?,以此证明w与v、k在同一平面内,且与v夹角为θ。
我们举个最简单的例子:把点P(1, 0, 1)绕旋转轴u = (0, 1, 0)旋转90°,求旋转后的顶点坐标。 1、 首先将P扩充到四元数,即p = (P, 0)。 q = (u*sin45°, cos45°)。求 1、 的值。 建议大家一定要在纸上计算一边,这样才能加深印象,连笔都懒得动的人还是不要往下看了。 3、最后的结果p` = ((1, 0, -1), 0),即旋转后的顶点位置是(1, 0, -1)。
如果想要得到复合旋转,只需类似复合矩阵那样左乘新的四元数,再进行运算即可。
我们来总结下四元数旋转的几个需要注意的地方: 1、用于旋转的四元数,每个分量的范围都在(-1,1)。 2、每一次旋转实际上需要两个四元数的参与,即q和q*; 3、所有用于旋转的四元数都是单位四元数,即它们的模是1;
欧拉角到四元数的转换
四元数到欧拉角的转换
arctan和arcsin的结果是 那么,在实践中是怎样的呢?我们接下来先了解一些名词。
AHRS是自动航向基准系统(Automatic Heading Reference System)的简称。目前,使用四元数来进行AHRS姿态解算的算法被广泛采用于四轴飞行器上。该算法源自英国Bristol大学的Ph.D Sebastian Madgwick,他在2009年开发并发布了该算法。下面我们来对该算法的代码进行详细分析。
IMU是惯性测量装置(Inertial Measurement Unit)的简称,通常包含陀螺仪和加速度计。(MPU9150还包括磁力计)
现在,让我们回到姿态解算代码的分析。下述代码的核心思想是:通过陀螺仪的积分来获得四轴的旋转角度,然后通过加速度计的比例和积分运算来修正陀螺仪的积分结果。
重力加速度归一化(规范化)(normalization),就是转化为标量,即只有数值大小,没有方向,在IMU中是将三维向量转化成单位向量,因为单位矢量到参考坐标系的投影,所以要把加速度计数据单位化,
四元数表示转动,首先其模应该为1,
下面代码中的gx,gy,gz分别代表陀螺仪在X轴,Y轴和Z轴三个轴上的分量,ax,ay,az分别代表加速度计在在X轴,Y轴和Z轴三个轴上的分量。
void MahonyAHRSupdateIMU(float gx, float gy, float gz, float ax, float ay, float az) {
float recipNorm; //归一化、规范化的中间变量
float halfvx, halfvy, halfvz; //重力的值
float halfex, halfey, halfez; //偏差程度
float qa, qb, qc;
只有当加速度计测量有效时才计算反馈(避免在加速度计正常化时使用NaN)
// Compute feedback only if accelerometer measurement valid (avoids NaN in accelerometer normalisation)
if(!((ax == 0.0f) && (ay == 0.0f) && (az == 0.0f))) {
invSqrt为平方根的倒数,原因是使得下面的ax,ay,az的运算速度更快。通过归一化处理后,ax,ay,az的数值范围变成-1到+1之间。
归一化化加速度计测量
// Normalise accelerometer measurement
recipNorm = invSqrt(ax * ax + ay * ay + az * az);
ax *= recipNorm;
ay *= recipNorm;
az *= recipNorm;
根据当前四元数的姿态值来估算出各重力分量。用于和加速计实际测量出来的各重力分量进行对比,从而实现对四轴姿态的修正。
// Estimated direction of gravity and vector perpendicular to magnetic flux
halfvx = q1 * q3 – q0 * q2;
halfvy = q0 * q1 + q2 * q3;
halfvz = q0 * q0 – 0.5f + q3 * q3;
使用叉积来计算估算的重力和实际测量的重力这两个重力向量之间的误差。
// Error is sum of cross product between estimated and measured direction of gravity
halfex = (ay * halfvz – az * halfvy);
halfey = (az * halfvx – ax * halfvz);
halfez = (ax * halfvy – ay * halfvx);
把上述的累计误差进行积分运算,就可以消除累积误差。
// Compute and apply integral feedback if enabled
if(twoKi > 0.0f) {
integralFBx += twoKi * halfex * (1.0f / sampleFreq); // integral error scaled by Ki
integralFBy += twoKi * halfey * (1.0f / sampleFreq);
integralFBz += twoKi * halfez * (1.0f / sampleFreq);
gx += integralFBx; // apply integral feedback
gy += integralFBy;
gz += integralFBz;
}
else {
integralFBx = 0.0f; // prevent integral windup
integralFBy = 0.0f;
integralFBz = 0.0f;
}
把上述计算得到的重力差进行比例运算。比例的结果累加到陀螺仪的数据中,用于修正陀螺仪数据。比例系数为Kp。
// Apply proportional feedback
gx += twoKp * halfex;
gy += twoKp * halfey;
gz += twoKp * halfez;
}
至此,我们得到了修正后的数据,然后我们需要将这些数据,表示到四元数中。
// Integrate rate of change of quaternion
gx *= (0.5f * (1.0f / sampleFreq)); // pre-multiply common factors
gy *= (0.5f * (1.0f / sampleFreq));
gz *= (0.5f * (1.0f / sampleFreq));
qa = q0;
qb = q1;
qc = q2;
//一阶近似算法
q0 += (-qb * gx – qc * gy – q3 * gz);
q1 += (qa * gx + qc * gz – q3 * gy);
q2 += (qa * gy – qb * gz + q3 * gx);
q3 += (qa * gz + qb * gy – qc * gx);
把上述运算后的四元数进行归一化处理。得到了物体经过旋转后的新的四元数。
// Normalise quaternion
recipNorm = invSqrt(q0 * q0 + q1 * q1 + q2 * q2 + q3 * q3);
q0 *= recipNorm;
q1 *= recipNorm;
q2 *= recipNorm;
q3 *= recipNorm;
}

我是一个粉刷匠,粉刷本领强。
|
|




 发表于2018-10-25 15:20:59
发表于2018-10-25 15:20:59


















 收藏
收藏